Relative interior
In mathematics, the relative interior of a set is a refinement of the concept of the interior, which is often more useful when dealing with low-dimensional sets placed in higher-dimensional spaces. Intuitively, the relative interior of a set contains all points which are not on the "edge" of the set, relative to the smallest subspace in which this set lies.
Formally, the relative interior of a set S (denoted 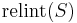 ) is defined as its interior within the affine hull of S.[1] In other words,
) is defined as its interior within the affine hull of S.[1] In other words,
where 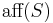 is the affine hull of S, and
is the affine hull of S, and 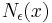 is a ball of radius
is a ball of radius  centered on
centered on  . Any metric can be used for the construction of the ball; all metrics define the same set as the relative interior.
. Any metric can be used for the construction of the ball; all metrics define the same set as the relative interior.
For convex sets C the relative interior can be defined:
See also
References
- Boyd, Stephen; Lieven Vandenberghe (2004). Convex Optimization. Cambridge: Cambridge University Press. p. 23. ISBN 0 521 83378 7. http://www.stanford.edu/~boyd/cvxbook/.
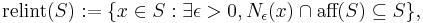
![\mathrm{relint}(C)�:= \{x \in C�: \forall_{y \in C} \exists_{z \in C} \exist_{\lambda \in ]0,1[} x=\lambda y %2B (1-\lambda) z\}](/2012-wikipedia_en_all_nopic_01_2012/I/ccb9571a908f2a9830c3ffa71f1330c6.png)